Introduction
This article discusses various biophysical concepts that are important to understand and gain an intuitive understanding of the functioning of the cardiovascular system. Nature offers great symmetry and basic physical laws determining the pressure, surface tension, and flow in elastic pipes can be used to gain insight into the functioning of the cardiovascular system.
Conventional teaching fails to establish a proper link between elementary physical laws and the intricacies of the cardiovascular system. Concepts such as Laplace’s law, Bernoulli’s equation, Windkessel model, elastic waves, and flow dynamics in elastic tubes should be introduced in first-year physiology lectures to make it easier for students to understand the origins of blood pressure, factors that can affect blood pressure in vascular segments, pulse wave formation, and transmission.
Once these physiological principles are understood through physical laws, understanding the pathological processes and basis of pharmacological intervention in various cardiovascular diseases is also simplified.
The Origin of Pressure
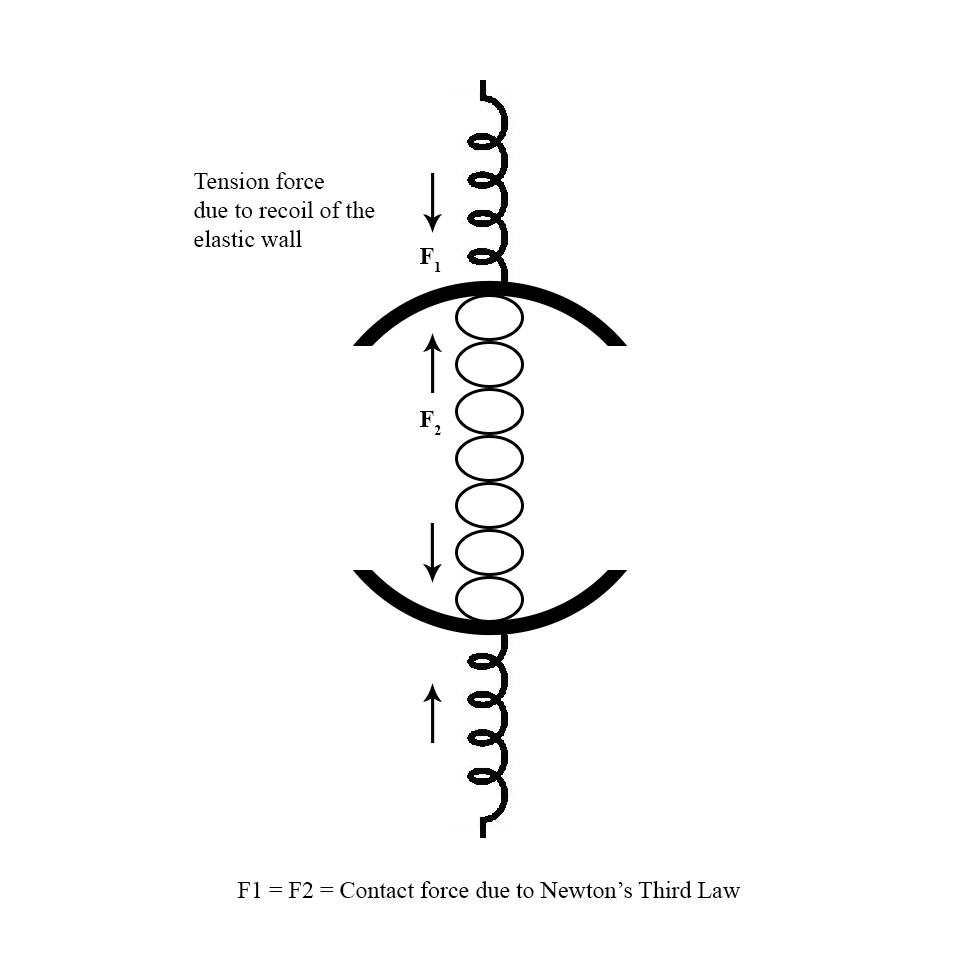
Imagine filling a balloon with an incompressible fluid such as water. As more fluid is added, the balloon expands to create a greater space for an increased number of particles to fit inside. To accommodate the fluid molecules with the appropriate intermolecular spacing, the particles push against the balloon wall and stretch it; consequently, passive tension develops in the wall. The balloon wall tends to recoil back to its original unstretched position. In doing so, it presses on the fluid inside and exerts a compressing force on the particles. The inward elastic recoil force is balanced by a force originating from the fluid or material that opposes further deformation and counters the recoil tendency of an elastic wall. 1, 2
Figure 1
The inward recoil tendency of the elastic wall is counterbalanced by the development of excess pressure force in the fluid. At equilibrium, the tendency of the contents to recoil outwards is equal to the tendency of the wall to contract or recoil inwards
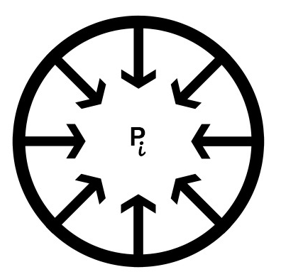
Thus, pressure is the consequence of a contact force that arises when a certain volume of material or mass is placed in a stretched elastic compartment. This is an example of Newton’s third law (action-reaction pair), wherein the stored contents tend to recoil outwards or expand against a stretched elastic wall and are acted on by an equal reaction force from the wall.
Figure 2
Development of an action-reaction pair between the elastic walls and the contents stored in the cavity. The tension in the elastic wall maintains the high pressure of the stored contents
The pressure of a flowing fluid can be divided into static and dynamic parts. Static pressure is the pressure measured when the fluid is stationary. A component of the static pressure results from the elastic forces exerted by the wall, and the other component is provided by the weight of the overlying fluid particles.3
Dynamic pressure is the pressure in a moving fluid and is dictated by Bernoulli’s equation. This equation relies on the principle of energy conservation and enables the interconversion of energy in an ideal flowing fluid.4
Figure 3
Principle of Bernoulli’s equation, based on the concept of interconversion of energies in a flowing fluid. Bernoulli’s equation contributes to changes in dynamic pressure in an ideal flowing fluid
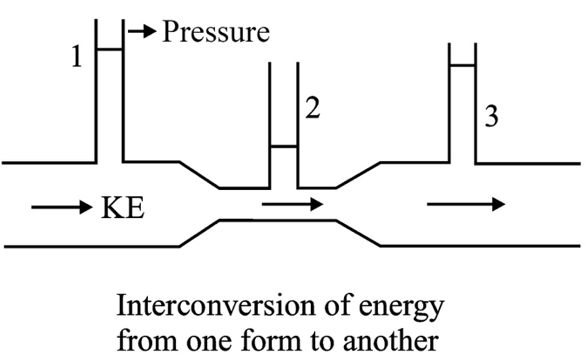
If the fluid encounters a sudden reduction in the cross-sectional area, the velocity increases accordingly to maintain the same flow rate across the narrower tube.
The drop in pressure from a wide to narrow tube provides an adequate force to accelerate the fluid mass as it travels through the tube with a decreased cross-sectional area.
However, if the fluid is transitioning from a narrow to a wider tube, as per the equation of continuity, the flow velocity must fall to maintain the same flow rate. This implies that the flow must travel against an adverse pressure gradient to decelerate and reduce its velocity. Therefore, the pressure must increase as the fluid flows from the narrow tube to the wider tube.
From an energy point of view, the fluid velocity must rise while transitioning from a wide to a narrow pipe, leading to a concomitant increase in kinetic energy. Because the system’s total energy remains the same, an increase in kinetic energy is sustained by a decrease in the pressure potential energy of the flowing fluid.
Therefore, Bernoulli’s equation establishes an inverse relationship between lateral pressure and velocity at a given point, which is an important factor in determining the dynamic pressure of a flowing fluid.
Pressure, Tension and Radius—Law of Laplace
Law of Laplace provides the quantitative understanding between the tangential wall stress and the intraluminal pressure in an elastic sphere/cylinder.
In an elastic vessel, the intraluminal pressure is determined by the tension, radius and the wall thickness of the vascular segment as given by the following relation.
Figure 4
Law of Laplace dictates that intraluminal pressure is directly proportional to tangential wall stress, wall thickness and inversely proportional to radius of curvature.(P= Pressure, W= Wall Thickness, T= Tension, R= Radius)
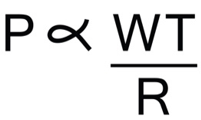
Originally, used to describe generation of pressure in spherical bubbles, this law is extrapolated to elastic spheres and cylinders in the human body such as the alveoli and blood vessels.
As, pressure generated in a vascular segment, is directly proportional to the tangential wall stress or tension, a detailed insight into the factors determining wall tension, will help us to understand how these factors link to modify vascular pressures.
Distensibility of the vascular segment
The passive wall tension developed for a certain degree of stretch is dependent on the stiffness of the arterial segment; a segment with greater stiffness will develop a higher wall stress, thus exerting a greater inward radial component on the incompressible blood mass. This allows the stiffer arterial segments to exert a greater pressure for a given blood volume/wall stretch.
The distensibility of a vessel wall not only changes from vessel to vessel but also varies with the volume of blood in a particular vessel. Increased volume, leading to increased pre-stretch, makes the arterial wall progressively stiffer and allows for an increased passive recoil force.
Volume of blood in the vascular segment
The volume of blood in a vascular segment dictates the degree to which the arterial wall is stretched; as mentioned earlier, the wall stiffness increases with a higher degree of stretch. Thus, the tangential wall stress increases with increasing volume, allowing for a rise in vascular pressures with greater volumes.
The volume or stretch in the arteries is determined by the difference in the rates of influx and outflow of blood from the central aorta to the peripheral compartment. While the outflow rate depends on peripheral vascular resistance, the inflow rate depends on cardiac parameters such as contractility and preload. These factors influence the velocity and force of cardiac contraction, thereby regulating the volume the heart ejects in one cardiac cycle.
Effect of curvature on pressure—The two balloon experiment
The next component which influences vascular pressure is the curvature/radius of the segment.
For a given wall stress, the radius of the segment determines the effective radial component of wall stress which generates vascular pressures.
Let us understand how curvature determines vascular pressure using a demonstration/experiment.
If two balloons, one with a larger and the other with a smaller radius, are interconnected, one might intuitively assume that the gas will flow from the larger to the smaller balloon. However, contrary to intuition, the smaller balloon shrinks further in size. This suggests that the pressure in the smaller balloon was higher than that in the larger balloon, allowing a sufficient pressure gradient to move air from the smaller to the larger balloon.1
The larger balloon has a lower pressure even though the volume of gas within it is higher than that of the smaller balloon. Thus, the collapsing tendency of the balloon on the gas/medium depends on the degree of the stretch and the geometry of the balloons. Laplace’s law expresses this relationship.
Two balloons with the same tension but different radii exerted different forces on the enclosed substances. A balloon with a larger radius has a smaller inward tension component. Therefore, the pressure in a large balloon is lower than that in a balloon with a smaller radius. Thus, for the same tension, a balloon with a smaller radius will have a larger magnitude of tangential stress directed toward the cavity, resulting in higher pressure.
Figure 7
Pressure in a balloon depends on its tension and curvature. For the same wall tension, a balloon with a larger radius will have a smaller inward component of tension force, generating less pressure. Thus, intraluminal pressure is dependent on the wall tension and the curvature of the balloon (Law of Laplace)
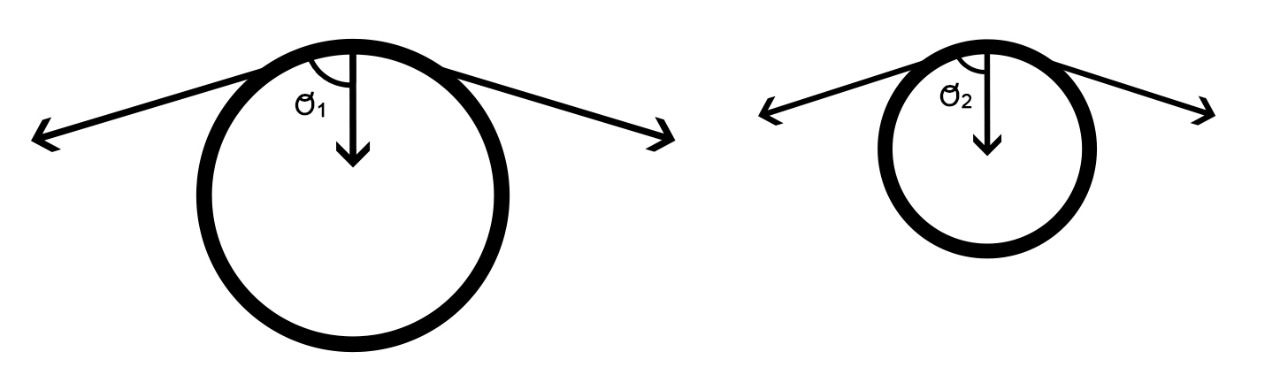
Thus, owing to the higher pressure in the smaller balloon, air flowed from the smaller to the larger balloon until the pressure equilibrated.
Aneurysm formation—Balloon and arteries
The pressure–volume (P–V) curve for a balloon is similar to that shown in Figure 8. The pressure initially increases when the radius is small and then plateaus as the radius continues to increase.5 With further stretching, there is a sudden increase in the stiffness of the balloon, which increases the elastic recoil force and raises the intraluminal pressure. This P–V curve explains the peculiarity of the decrease in pressure with increasing radius.
Figure 8
Pressure–volume curve for an elastic balloon. A volume increase causes an initial pressure increase, after which it falls and plateaus over a range of wall stretch or volume. With a further increase in stretch or volume, the pressure suddenly increases. This is in contrast to the response noted in an artery on increasing wall stretch or volume
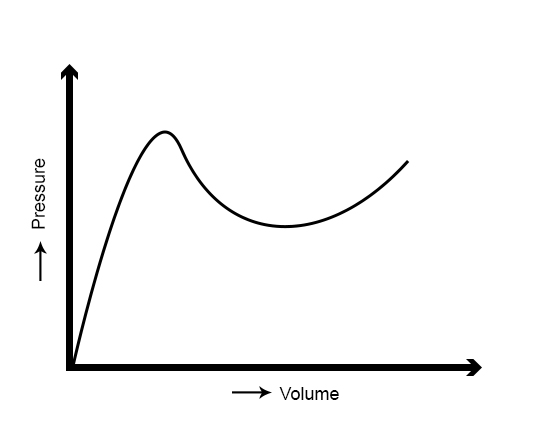
However, an artery does not exhibit this elastic behavior. With progressive inflation, the artery unlike a balloon becomes stiffer, causing a rise in the resistance to lateral stretch or transverse displacement of the vessel wall with rising radius.
This difference between an artery and a balloon is attributed to the elastic properties of the arteries. An artery is made from a mixture of elastin and collagen fibers that have different Young’s moduli and are recruited at different degrees of stretch. At lower amounts of stretch, less stiff/more abundant elastin fibers were recruited; at higher amounts of stretch, stiffer collagen fibers were recruited.6
This makes an artery behave differently from a cylindrical balloon and helps prevent the formation of local dilatations or aneurysms, such as those observed in a cylindrical balloon. In contrast to a balloon that offers less resistance to stretching with increasing size/radius, allowing for almost complete expansion of one area before moving to the next, an artery becomes progressively stiffer as it is stretched, which prevents the formation of local bulges or aneurysms as blood is pumped into each vascular segment.7
Laplace’s law dictates that for constant stiffness of the elastic chamber, pressure is inversely proportional to radius. However, in an artery another factor plays an important role which offsets the fall in pressure with increasing radius. The pressure volume curve of an artery allows for increasing stiffness with greater radii, allowing the artery to compensate for the fall in pressure, as predicted by Law of Laplace.
If arteries are not equipped with this mechanism, then like a cylindrical balloon, the area which is stretched previously, will offer lesser resistance to further stretch and will almost completely expand, before moving on the next segment. However, as an artery expands, the resistance to further stretch increases and prevents the development of local bulges or aneurysms under normal physiological circumstances.
Arterial Windkessel: Aorta and Peripheral Resistance
The functional arrangement of the aorta and arterioles (sites of total peripheral resistance) is comparable to that of the Windkessel model, which describes the arrangement of an air chamber connected to a set of rigid pipes. When attached to a pulsatile source of fluid current, the unsteady current input is converted into a continuous, steady flow. If the arterial system had rigid pipes, the peripheral flow would have followed ventricular ejection, leading to a sharp rise in current output during systole and an instantaneous fall or cessation of current during diastole.8
The arterial Windkessel works on the following concept.
As blood is intermittently and periodically pumped into the arterial tree during systole, some of the current is stored in the elastic aorta before exiting through the peripheral resistance. This creates some stretch and allows the blood volume to experience a circumferential passive recoil force/passive squeeze, which raises the upstream vascular pressure and forces the blood volume through the peripheral arteriolar resistance ahead. This rise in aortic pressure and the corresponding rise in systolic current occurs steadily and gradually, thus converting a sudden input current into a slowly rising output current through the arterioles.
As the ventricles cease to contract and enter the diastole, the force which counteracts the passive recoil force of the elastic aortic wall is interrupted. This allows the elastic aortic wall to return to its original position, squeezing the stored blood mass and pushing it through the arterioles, thus maintaining perfusion even during ventricular diastole.
If the aorta loses its compliance and becomes a stiff, rigid pipe, the rise and fall of aortic pressure would be very similar to that of the left ventricle. This means that there will be a sudden pulsatile burst of systolic current, which will be transmitted almost instantaneously into the peripheral microcirculation, leading to end-organ damage.9
The aortic pressures would rise swiftly, abruptly, and to a greater extent during a single heartbeat, which would increase the left ventricular afterload. A stiffer aorta signifies a greater resistance to lateral stretch and transverse displacement of the aortic wall, which lowers the capacity of the aorta to store blood volume. Hence, the blood volume released during diastole reduces, leading to a decrease in the diastolic pressure and hampering effective coronary perfusion.10
Pulse and Signals
Consider an elastic medium in which a push or pull applied at one end is not immediately transmitted through the entire medium. Rather, it takes a finite time to travel from one end to another via the formation of local interactive signals between adjacent molecules. A pulse wave is a means of transferring momentum from one particle to another in an elastic medium.11
Figure 9
In an elastic medium, momentum transfer occurs via the formation of local interactive forces which serve to transmit the impulse from one particle to another. The entire process happens at a characteristic velocity, hence, an impulse applied at one end is received at the other end after some delay
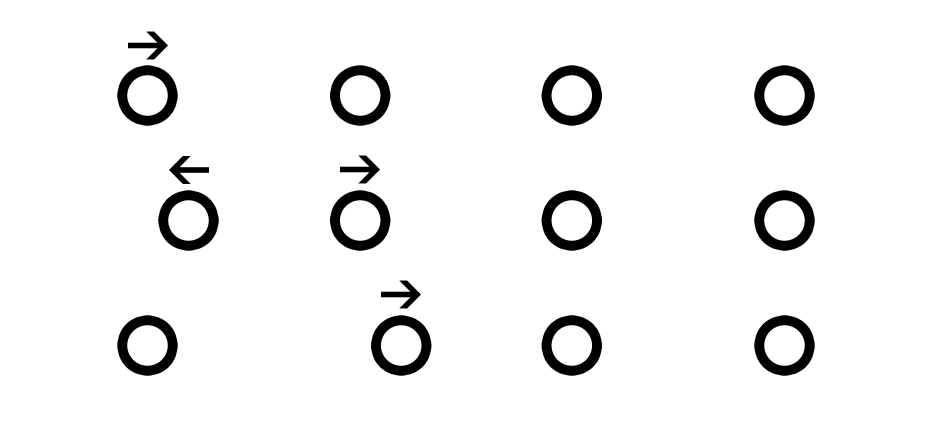
The arterial tree can be considered to consist of an infinite number of coupled oscillators that allow for the propagation and transmission of a pressure-volume wave, shunting blood from one segment to another to create space for the newly ejected blood volume. The pulse signal is generated by the linear superposition of various harmonic frequencies and signals the distal sites of the cardiac systole/ejection of blood volume.12
As soon as the blood is pumped in, the proximal part expands and develops tension, allowing for an increase in pressure and ensuring an adequate pressure signal to overcome the inertia of the pre-existing blood volume. This leads to a shunting phenomenon, and the blood rapidly moves from one segment to another, liberating the arterial tree of the previously occupied blood volume.
The rate at which this push signal or pressure-volume wave propagates is known as the pulse-wave velocity. Understanding the rate at which an elastic wave propagates provides insight into the stiffness and elasticity of the medium through which the wave propagates. Similarly, pulse wave velocity helps us to understand the mechanical properties of arterial trees.
As blood is pumped into the most proximal aortic segment, it takes finite time and volume to stretch the elastic vessel wall sufficiently to generate a sufficient elastic recoil force and increase the local pressure to generate the push signal for mobilization of the adjacent segment. If the vessel is less distensible, the desired push signal can be generated rapidly with less delay, and the pre-existing column of blood can be quickly mobilized to liberate space for the incoming blood volume.13
Therefore, pulse wave velocity can be used to assess the stiffness or rigidity of an arterial segment. The signal velocity should not be confused with the blood-flow velocity. Flow velocity is the velocity at which the blood mass moves from one segment to another while receiving the push signal. Subsequently, the pulse wave velocity determines the speed at which the push signal rises in a segment and the rate at which the fluid mass reacts to this push signal.
Pulse Wave Reflection: Consequence of Impedance Mismatch
A discontinuity occurs when the wave reaches the junction between two different media. The particle at the junction must transmit energy or a signal to a dissimilar particle in the next media. The particle is not completely receptive to the incoming wave of energy; hence, some of the energy is reflected towards the source owing to the underlying impedance mismatch. The phenomenon when a portion of the energy carried by an elastic wave is reflected upon encountering a discontinuity or site of impedance mismatch is known as reflection.
Pulse waves are reflected in the arterial tree whenever they encounter a site of impedance mismatch, which allows some energy to be reflected towards the source. The reflected wave carries information about the peripheral sites back to the source, which in this case, is the heart. The reflected wave carries information about the resistance sites and interacts with and superimposes on the forward wave to form a net resultant pressure and flow wave. At certain frequencies, however, the crests of the incident and reflected waves perfectly line up, creating a standing wave pattern, in which case the system is said to be in resonance.
Measuring the timing of the reflected wave is crucial for determining ventricular afterload. If the reflected pressure wave reaches early during systole, it will constructively interfere with the forward wave, and the pressure in the aorta will rise, leading to an increased load against which the heart is pumping blood. Thus, an increased pulse wave velocity allows the reflected pressure signal to reach the proximal aorta sooner than normal, leading to a magnification of the pressure amplitude.14
Discussion
This article highlights the symmetry present in nature concerning basic physical laws and attempts to bridge the gap between elementary physics and applied physiology. Natural laws such as the Law of Laplace, which governs pressure-tension relationships in an elastic balloon, can describe pressure–tension relationships in an artery. The addition of blood volume to elastic vessels expands and stretches them, leading to the formation of a contact force, forming the biophysical basis of vascular pressure. Bernoulli’s equation and the equation of continuity can be used to determine dynamic blood pressure. These physical laws are implicated in pathological conditions, such as abnormal vascular dilation (aneurysms) and stenosis. To better understand the pressure–flow relationships, the arrangement of the aorta and resistance vessels can be compared with that of a Windkessel.
Momentum and signal transfer in an elastic medium via an elastic wave, such as a sound wave, is analogous to transmitting a signal via a pressure–volume pulse wave in the arterial system. Noninvasive methods of measuring pulse wave velocity provide insight into the stiffness of the vascular segment and can be explored for various therapeutic and prognostic purposes.14
Article DOI
